Este esquema clasifica los idiomas generados por gramáticas en cuatro categorías:
Regulares
Libres de contexto
Sensibles al contexto
Recursivamente enumerables
Para cada una de ellas, hay un autómata que puede reconocer oraciones en el idioma:
Autómata finito, también conocido como máquina de estados finitos
Autómata con pila
Autómata linealmente acotado
Máquina de Turing
Los idiomas naturales pertenecen a los tipos de gramática más poderosos, y la máquina que corresponde a ellos es la máquina de Turing.
Ahora presento un ejemplo de un idioma común, la clase más simple, para ilustrar esta impresionante correspondencia entre gramáticas y máquinas. Consideremos esta gramática:
ORACIÓN-> “La” PARENTESCO “es” ADJETIVO
PARENTESCO-> RELACIÓN “de” PERSONA
RELACIÓN-> “madre” | “padre” | “hermana” | “hermano” | “hijo” | “hija”
PERSONA-> “Ana” | “David”
ADJETIVO-> “brillante” | “grande”
Con ella, podemos crear oraciones tan inspiradoras como “La mamá de Ana es brillante” y “La hija de David es grande”.
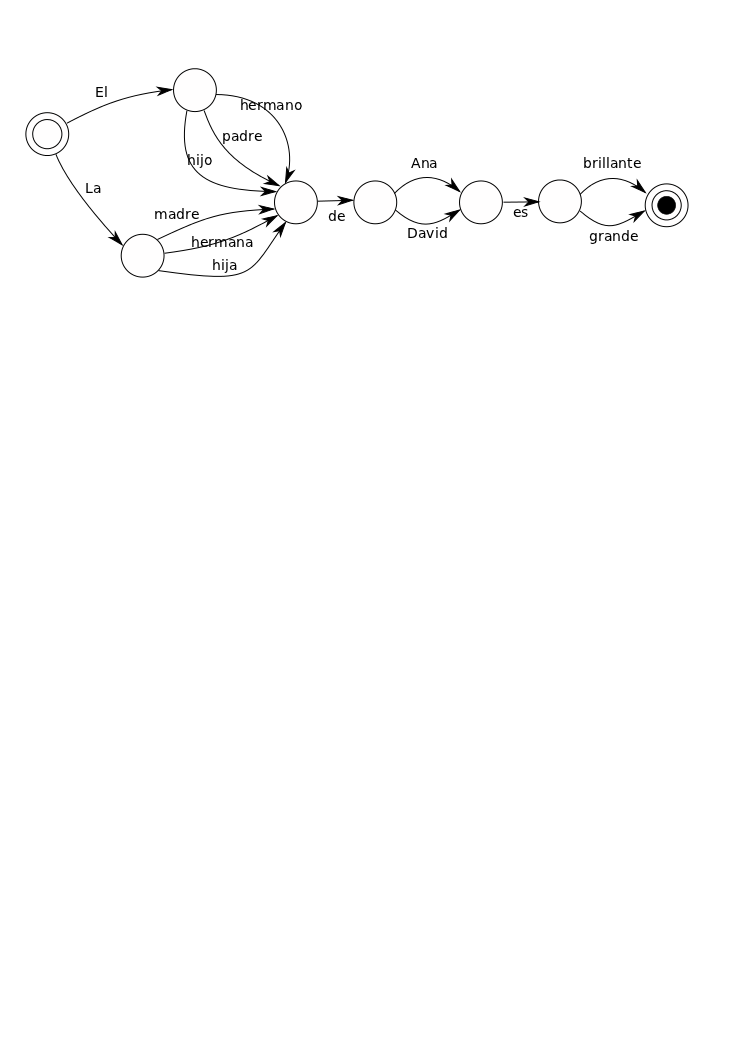
La correspondiente máquina de estados finitos reconoce estas dos oraciones, más las otras 22 que pueden crearse con ellas (escribirlas queda como ejercicio divertido para el lector). Consta de una cantidad de estados unidos por flechas etiquetadas que representan transiciones de un estado a otro. Hay un estado inicial especial y otro estado final especial:
Sería muy fácil confundirse en este punto y creer que “finito” en máquina de estados finitos se refiere al hecho de que sólo un número finito de oraciones pueden producirse o reconocerse. Este no es el caso en absoluto. Se refiere al hecho de que hay un número finito de estados (los círculos, siete en este caso). Al hacer una pequeña modificación de nuestra gramática podríamos crear oraciones de longitud arbitraria, incluso si el número de estados se deja inalterado.
ORACIÓN-> “El” PARENTESCO “es” ADJETIVO
PARENTESCO-> RELACIÓN “de” PERSONA
RELACIÓN-> “madre” | “padre” | “hermana” | “hermano” | “hijo” | “hija”
PERSONA-> “Ana” | “David” | “el” PARENTESCO
ADJETIVO-> “brillante” | “grande”
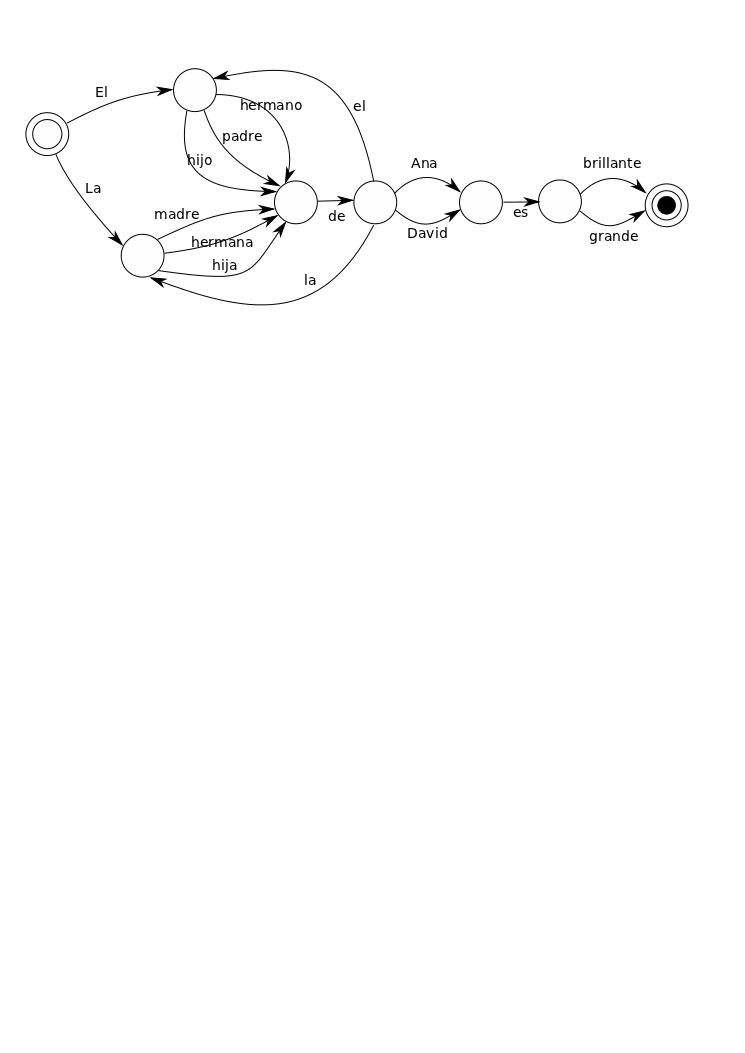
Hemos agregado “el” PARENTESCO como una alternativa más para PERSONA. En la máquina de estado finito aparece sencillamente como una nueva flecha que vuelve al segundo estado.
Ahora podemos crear oraciones como “El hijo de la hermana de la madre de la hija de David es alto”. Solía jugar este juego con mis ex amigos (se convertían automáticamente en ex amigos en el momento en que empezaba a jugar este juego con ellos). Cuando hablaba de mi hermano, por ejemplo, me refería a él como el hijo de la tía de la hermana de mi primo.
La jerarquía Chomsky ha sido estudiada mucho desde ambos campos. En la informática brinda las bases de la sintaxis para lenguajes de programación, entre otros. Se ha puesto mucho esfuerzo en tratar de capturar la estructura de los idiomas reales como el inglés con las gramáticas y sus correspondientes máquinas para muchos propósitos, entre ellos la traducción. Los sistemas de traducción basados en este enfoque se conocen como “basados en reglas”.
Traducción del original de Pablo A.